“A good programmer is someone who always looks both ways before crossing a one-way street.”

509. Fibonacci Number

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.

Given n, calculate F(n).

Example 1:

Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

相信大家都用遞迴寫過費氏數列的題目：

class Solution(object):
    def fib(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n <= 1:
            return n
        
        return self.fib(n - 1) + self.fib(n - 2)

記憶化遞迴：

class Solution(object):
    def fib(self, n, memo={}):
        """
        :type n: int
        :rtype: int
        """
        if n in memo:
            return memo[n]
        if (n <= 1):
            return n
        memo[n] = self.fib(n - 1, memo) + self.fib(n - 2, memo)
        return memo[n]
        

比較一下普通遞迴跟記憶化遞迴的速度差異：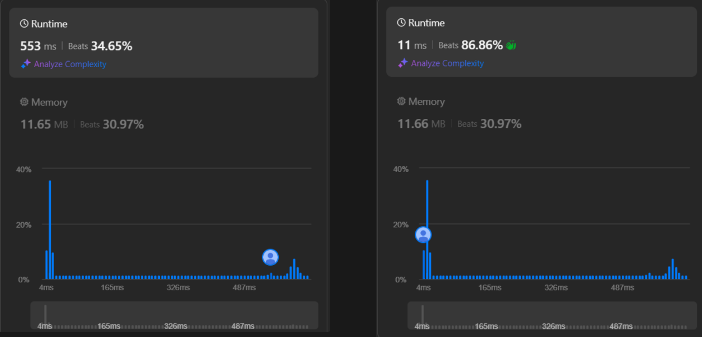

為什麼差那麼多?

因為普通遞迴重複計算了已經算過的值，舉例來說fib(5) = fib(4) + fib(3)，再繼續往下拆解，

fib(4) = fib(3) + fib(2)，有發現了嗎?又算了一次fib(3)，因為遞迴內的子函數不知道外面有已經算好的值。

記憶遞迴透過把算過的值記錄下來，一旦發現已經算過了，那就直接拿算過的值回傳！

什麼是動態規劃?

剛剛的遞迴是由頂向下的(fib(5)一層一層拆到fib(1)和fib(0))，而且需要我們手動去做記憶。

而動態規劃是由底向上的，而且自帶記憶！

class Solution(object):
    def fib(self, n, memo={}):
        """
        :type n: int
        :rtype: int
        """
        if n <= 1: # 如果n是0或1，會導致下面迴圈越界！
            return n
        dp = [0] * (n + 1)
        dp[0] = 0 # 初始條件
        dp[1] = 1 # 初始條件
        for i in range(2, n + 1):
            dp[i] = dp[i - 1] + dp[i - 2]
        return dp[n]

70. Climbing Stairs

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:

Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

題目問說一次爬1-2層，爬到第n層有幾種爬法?

當遇到很複雜的題目時，想從小的測資開始慢慢帶，看有沒有規律存在：

• n = 2，答案是2
• n = 3，答案是3
• n = 4，答案是5
• n = 5，答案是8

有沒有感覺就是費氏數列?但為什麼是費氏數列?

題目說一次可以爬1層或2層，所以爬到第4層的時候一定是從第3層或第2層爬上來的，爬到第5層的時候一定是從第4層或第3層爬上來的，這就是為什麼是費氏數列！

class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        if (n <= 1):
            return n
        dp = [0] * (n + 1)
        dp[1] = 1
        dp[2] = 2
        for i in range(3, n + 1):
            dp[i] = dp[i - 1] + dp[i - 2]
        return dp[n]